あたまがいい
|
|
|||||||||
|
|
|||||||||
|
あまり難しいとウンザリするので簡単な例を出してみましょう。 小学校の算数です。
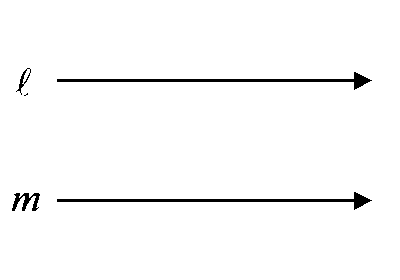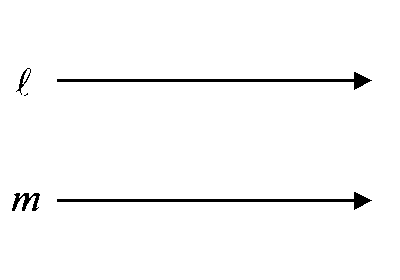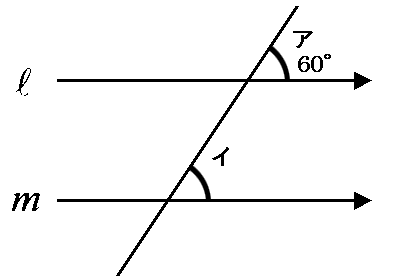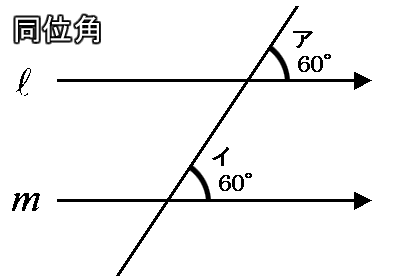
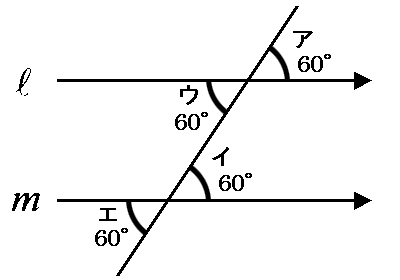
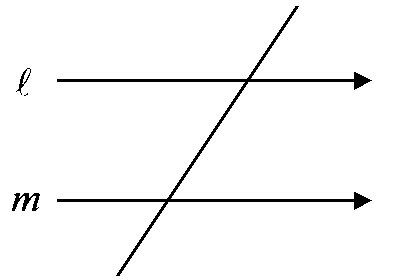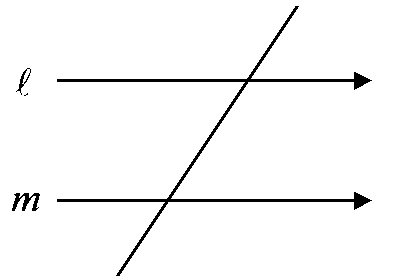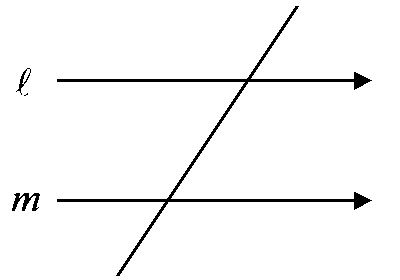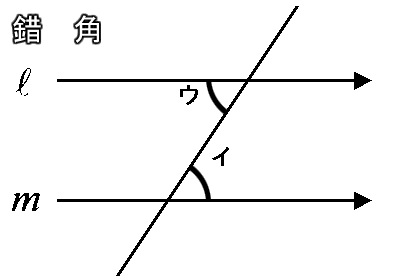
◆知識◆ 直線 l と m が平行の時、この2本の直線に交わる直線がつくる角アと角イは同じ角度になります。 これを『同位角』と言います。
って、小学校の時に習いましたよね(名称は中学校で学習)? 忘れちゃいました? 懐かしいですよね。 そして、その角と向かい合う角、角アと角ウ、角イと角エ、これも同じになります。 これを『対頂角』と言いました。
…ってぇことは、早い話が角ア、角イ、角ウ、角エは全て同じってことです。
なら、角ウと角イの2つのペア、これにも名前がついていそうですね。 そう。これが『錯角』です。
思い出しました?
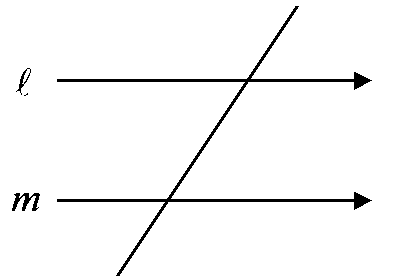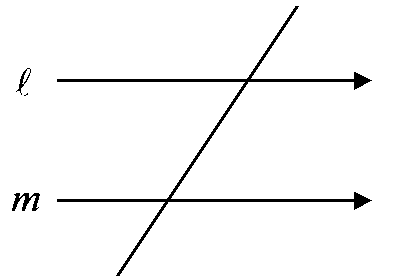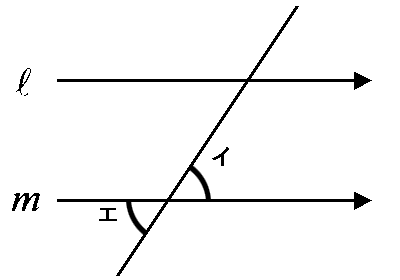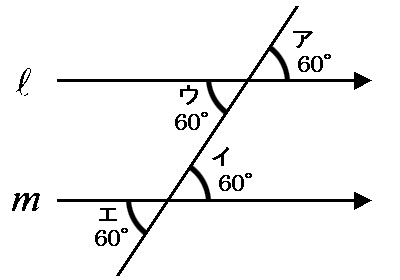
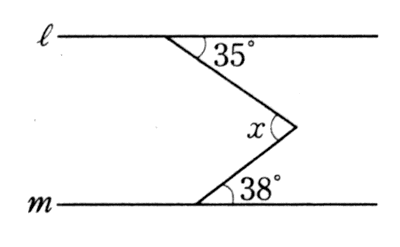
さて、それでは、この性質を頭に入れて、次の図の角X(エックス) を求めてみましょう!
◆問題◆
先へ進む前に、暫く悩んで下さい。
如何ですか? もう忘れてしまいましたか? 降参ですか?
では、答えの解説と行きましょう。
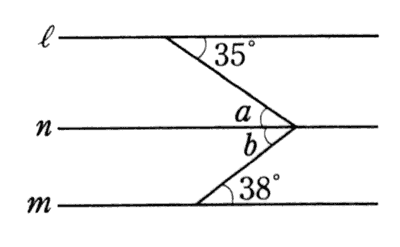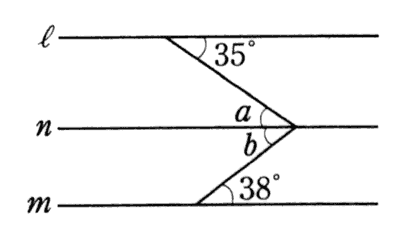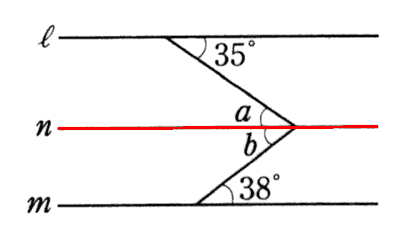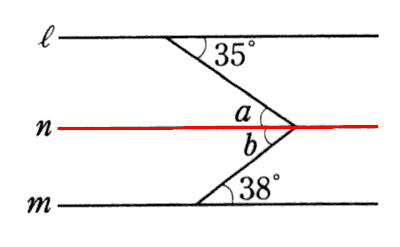
◆解説◆ この図をただ眺めていただけでは答えは出ません。 下のように角X(エックス)の頂点を通って、直線 l と m に全く平行な直線(n)を入れてみましょう。
線を一本入れることですぐに分かると思います。如何でしょうか? 錯角は等しいから、 角a と【35°】は等しい。
∠a = 35°
また、同様に錯角は等しいから、角bと【38°】は等しい。
∠b = 38°
つまり、∠a と ∠b を足せばいいから、
35°+38°=73°
そうです。答えは73度です。
簡単ですね。
この問題を悩んでいる人を見て、頭の悪い受験生なら『簡単じゃん!こんなことも知らないの?』と感じたかもしれません。 『こんなものも出来ないの?馬鹿じゃん!』と思ったかもしれません。
しかし、その前によく考えてみましょう。
実は、この問題、本当は非常に難しい問題なのです。 おそらくほとんどの人が解けないでしょう。 特に、自分は頭がいいと勘違いしている受験生には、まず解けない問題でしょう。
それは、どういうことでしょうか?
『簡単だ!』と感じた方に問います。
あなたは、なぜ『簡単だ』と思ったのですか?
それは、自分の頭が良いからですか? よくよく自分を振りかえって下さい。なぜ簡単なのですか?
そう、『教えてもらったから簡単』なのです。
『こんな問題も分からないのか?』と感じたあなたも振り返って下さい。 この問題と初めて出会った時、あなたは自分から答えを導き出しましたか? そうではなく、『ここに線を引くと分かるよ』と、先生に教わったから簡単なんじゃないですか? 教えてもらえばどんな馬鹿でも出来るようになります。 それは頭が良いことの証明でも何でもありません。 『教えられた』ことを覚えていたから簡単なのです。
『教えられた』から解けたのであって、 『頭がいい』から解けたのではありません。
本当に頭の良い人は、人に教えられなくてもあれこれ思考をくり返し、直線を引くことを発見し、正しい答えを導き出すことができます。『◆知識◆』の部分を教えただけで問題が解けてしまうのです。 やり方と答えを誰かに教えられなくても『与えられた条件から、自分で思考し、自分で判断し、正しい方法を見つけ、正解を導き出す』ことができるのです。こういう人間を『頭がいい』というのです。 無理? そんなことはありません。 あなたが無理なだけです。 現実には『頭がいい』人が沢山います。 やり方と答えを教えずとも自分で正解を導く小学生は沢山います。何人に1人という統計を出したことはありませんが、必ず『頭の良い子』はいます。私が授業する時、『これだけで解けたらジュースをおごるぞ!』と宣言し、今までに何本おごらされたことか!! やり方と答えを教えずとも解けてしまう能力を、『ひらめきがある』とか『カンが鋭い』なんて言い方もします。しかし、何もないところからひらめいたりはしません。普段から『思考』の訓練をして、初めて『ひらめき』も得られるのです。 思考の訓練もせず、ただ教えられたことを覚えて来た頭では、教えられた範囲のことだけでしか考えられません。そこからは、新しい発想や創造など生まれることはないでしょう。 一方、思考の訓練をした頭の良い人間なら、教えられたことだけに囚われず、あらゆる可能性を考え思考します。柔軟に、しかも自由に発想することができます。 そこに決定的な違いが存在します。 学習塾へ行けば問題の解き方を教えてくれます。それを真面目に聞いてくり返し努力すれば『お勉強』の成績は伸びるんです。けど、それは決して『頭が良くなる』ということではありません。よく勉強をすれば頭が良くなると勘違いをしている方がいますが、間違いです。ただ教わったことをくり返しできる能力がつくだけです。必ず『思考』という訓練が伴わなければ、頭は良くならないでしょう。
つまり、 『勉強が出来る』=『頭がいい』とは限らない のです。
…強いて言うなら、『説明が理解できるおりこうさん』という程度です(…って、教える側は、これが大変なんですが)。
これは一流大学の入試問題だろうが同じです。 当然、私がいきなり東大の数学の問題を見せられたって、解けるわけがありません。なぜなら、それにむけた『お勉強』をしていませんから。けど、ただただ教えられたことをひたすら覚え、お勉強を積み上げて行けば解けるのです。 別に最近流行っている『ドラゴンなんとか』の不良たちだけではありません。
頭をよくしたければ、それとは別に『考える』という訓練をしなければならないのです。 そして、その訓練は何も学校のお勉強に限ったことではないのです。いや、学校にしろ学習塾にしろ詰めこむので精一杯ですから、『考える訓練』かというと、はなはだ疑問です。 その証拠に、学校のお勉強が出来る奴ほど、ロクな思考が出来ない『馬鹿』ですから。
さて、今の話はあくまでも算数での話です。 ですから、やり方を教わるまで正解を導き出せなかったからと言って、『頭が悪い』とは断定できません。生理的に算数が嫌いな人もいれば、たまたま調子が合わない場合だってあるでしょう。 私がここで言いたいのは、あくまでも『やり方を教わらなくても、与えられた条件から思考して結果を導き出せる』人間が『頭がいい』ということです。その例として算数を出しました。 そう。 この能力を使うのは、算数だけではありません。あらゆるジャンルに通じています。その中の自分に合ったジャンルにおいて『自分の頭で考え、判断し、正しい答え』を導ければ良いのです。 実は、これが『小論文』で問われる能力なのです。 そして、今後の人生にも必要な能力なのです。 算数の問題には『正解』が用意されていますが、『小論文』の問題には『正解』が用意されていません。また、君たちの今後の人生には正しい答えが存在しません。いったい、誰が教えられるというのでしょうか?
小論文で言うなら、与えられたテーマに関する自分が学んだ知識・情報(前述の例で言うなら『同位角』『対頂角』『錯角』にあたるもの)を元に、正しい答え、つまり、自分の意見を『思考』するのです。 テーマが『国際化社会』なら、『同位角』『対頂角』『錯角』の変わりに『異文化に関する知識』が取って代わるのです。 これが小論文です。
人生で言うなら?…誰も教えてくれませんよ。 大人や先輩たちは、当然、君たちより長く生きています。だから、ある程度の知識と経験があり、アドバイスをすることができます。しかし、そのアドバイスが正しい保証などありません。人生に訪れる問題は、算数のように正しい解答が用意されてはいないからです。 最終的には自分で考え、判断しなければなりません。 アドバイスをくれた人の言うとおりにした結果、大失敗して、そのアドバイスをくれた人に抗議したところで、決して責任なんぞ取ってくれません。『おまえが悪い』と言われるだけです。 最後に頼れるのは、決断を下すあなた自身なのです。
自分の頭で考え、判断する能力…。 この能力こそが、あなたの人生を輝かせるのです。
2012年
|
|||||||||
|
|
||
|
|
||
|
|
||
|
||
| ■まえがき | ||
| ■予備校の先生 | ||
|
大学
|
||
| ■大学へ行こう! | ||
|
専門学校
|
||
| ■専門学校 | ||
|
コラム
|
||
| ■高校生諸君! | ||
| ■今の社会 | ||
| ■ローレライ | ||
| ■タッチ | ||
| ■ゆとり教育 | ||
| ■一流大学 | ||
| ■一休さん | ||
| ■あたまがいい | ||
| ■偏差値世代 | ||
| ■無限の可能性 | ||
| ■負け犬になる運命 | ||
| ■おかしな努力 | ||
| ■さらば宇宙戦艦ヤマト | ||
|
|
|
広 告
|
|
|
|
広告
|