![]()
流星物理のページに戻る
1.抵抗係数(drag coefficient)とは
少々専門的になりますが、流星の大気内での振る舞いを計算する上で、不可欠な定数のお話です。
物体に働く空気抵抗は、空気の流れに対する断面積と、大気密度、それに速度の2乗に比例して表されます。
そのときの比例定数が抵抗係数(drag coefficient)です。
抵抗係数は、その形状により大きく変化し、航空機や新幹線では、小さくなるように形状を工夫します。
さて、多くの文献では抵抗係数の量記号としてCDを使っていますが、
東ヨーロッパの文献では、Γという量記号も使います。注意が必要なのは、
CD/2=Γ
の関係があり、ちょっと誤解しやすい点です。
実際に計算すると、この抵抗係数の見積もりの差が、いくつかの結果に非常に大きな
影響を与えることがわかります。すなわち、より慎重に、正確な数値見積もりが要求される定数です。
ほとんど形状がわからない流星物質に対してなのですが・・・・
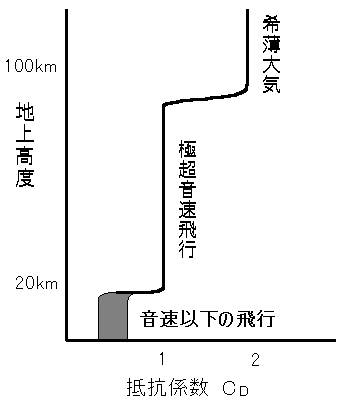
2.希薄大気(地上90km以上くらい)での抵抗係数
流星が地球に近付いて徐々に薄い大気に衝突する最初の領域です。
ここでは、大気分子同士がなかなか衝突できず、流星物質表面に衝突した大気分子は
鏡面反射し、速やかに流星物質から遠く離れた所へ飛んで行きます。
仮定した形状に対する積分計算をすれば、抵抗計算は容易に求めることができます。
形状として、球形を仮定すれば、
CD=2
となります。
3.超音速飛行(地上85km程度以下)での抵抗係数
大気密度が高くなって、流星物質表面に当たった大気分子が、遠く離れた所へ行く前に
他の大気分子と衝突を繰り返すようになると、抵抗係数も影響を受けます。
このとき、衝突した大気は、流星物質表面に垂直な速度ベクトルを失う、とモデル化できます。
このときも、仮定した形状に対する積分計算をすれば、抵抗計算は容易に求めることができます。
形状として、球形を仮定すれば、
CD=1
となります。
なお、希薄大気領域との境界は鮮明でなく、連続的ですが、
計算では不連続として扱うことが多いようです。
4.ダークフライト中の抵抗係数
隕石落下や、流星塵の落下を計算する場合は、音速以下の抵抗係数も知っておかなければなりません。
日常感覚に近い大気条件や速度条件ですが、最も見積もりが困難な領域です。
ほとんど同じ形状でも、表面のちょっとした凹凸が、物体回りの空気流れを変化させ、
抵抗係数に影響しますし、不安定な振動状態が起きることも珍しくありません。
流星物質の形状を球としたとき、私は、
CD=0.25〜1
程度の間の幾つかの数値を使って試算することが多いです。
隕石落下において、これまでの結果をまとめると、次の図のようになります。