きっかけ。
ただ単純に十二国記のシリーズを読んでいてて、「十二国記の世界って、どれくらいの大きさだろう?」ということから始まりました。大きさが把握できると、世界観も把握しやすいかなー? ってことで。
とりあえず自分で考えるよりも、ネットで誰か考えて載せている人がいないかなー? ってのを探してみました。
……探し方が悪かったのか、本気で考えている人が見つからなかったです。畜生!! だったら私が独断と偏見で考えてやるわい!!
本当にただコレだけです。 思いつかなきゃよかったよ、とほほ。
参考にしたもの。
とりあえず参考にしたのは、「黄昏の岸 暁の天」に出てくる六太の一言。
「こちらの一国ほどの広さではないさ。蓬莱そのものの広さをいうなら 」
もっとも、六太がどんな認識でこんなことを言ったのかは定かではないが、単純に「国土広さ」とさせていただきました。
あとは 「一国の大きさはほぼ同じ」ってのを採用しています。……ていうか、コレがないと始まらない……ともいう。島国もあることですし。
他にも「巧国を東西に端から端まで歩いて三ヶ月」とかいう記述があるけれども、起伏が多いだのなんだのってことを考えると、とても参考になるものとは思えず、このたびは排除しました。
だいたい「巧国を東西に端から端まで」って、どこのことを言っているのかもよくわからないし、三ヶ月歩き続けて一日平均何kmくらい歩けるか、の想像がいまいちつかなかったりしますから。
もう一つあって、内海を渡るのに3-4日(「月の影 影の海」より) というのが意外と頼りになりそうな記述なんですよね、コレが。
ただ、これも実はいまいちわからない……。帆船の速度なんて知らないし。
と思って調べたら、どうやら6ノットくらいみたいです。
ただ、コレはあくまで「最高に近い速度」であるのと、「帆船の構造によって変わる」ということ、さらに3-4日間の平均速度となると……なんともいえなくなります。
でも、「徒歩で三ヶ月」よりは指標にしやすいとは思いますが。
考え方。
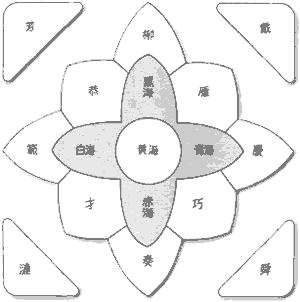
大雑把でもいいから「距離感」を掴みたいってのが当初の目的ですので、
もともと単純形状の十二国世界を、もっと単純化することにしました。
「私が計算できる単純図形の組み合わせ」に変形したというわけです。
黄海
コレはそのままの円。
 各極国
各極国
角が丸くても、直角二等辺三角形で。
 各大国
各大国
曲線を直線化。角を直角化。
そうしたら、正方形を三つ合わせた形に相成りました。
 各州国
各州国
コレも大国と同じく、 曲線を直線化し、角を直角化。
それだけでは計算を前提とすると求められない部分が出るので、
膨らんでいるところを二つあわせると
正方形になるという直角二等辺三角形にしてしまいました。
 変形合体!
変形合体!

相当強引かと思われますが、十二国世界地図とあわせてみても案外引けを取りません。
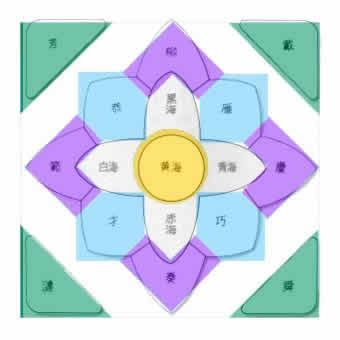
……うまい変形したもんだ!(自画自賛)
式。
「計算できる形」に変形したので、式が立てられるわけです。
てなもんで、 こんな式たちが成り立ちます。
黄海面積=(黄海半径)2π
極国面積=(極国等辺)2/2
大国面積=3×(大-州国境)2
州国面積=(州国海岸一辺)2 +(大-大国間距離)×(大-州国境)
さて。なんのこっちゃわけがわからないので、とりあえず色々整理してみると、下式になるんです。
黄海面積=X2π
極国面積=Y2/2
大国面積=3×X2
州国面積=Z2 +XZ√2 (すみません、√の中に「2」がうまく入りません……)
うーん、こっちもわからないね。どっちでもいいや。
ちなみに、各面積は「ほぼ同じ」という前提があります。
コレでわかるとおり、各面積を同じとして扱うと「π=3」になるんです!! ま、「ほぼ3」ってことなんですけど……
それでも、「徒歩で3-4ヶ月」や「帆船で3-4日」っていう誤差以上では出ないと思われます。25-33%も距離に違いが出るより、5%の差ですむんだもんね、「3」と「3.14」なら。
算出。
日本の広さはおよそ37万7千km2となっております。……すごいな、広辞苑って国土面積まで載ってるんだ、という感想はさておき。
「こちらの一国ほどの広さではないさ。蓬莱そのものの広さをいうなら 」(六太談)
という証言を参考にすると、
一国面積>37万7千km2
というわけです。
どれくらい「より大きい」のかの記述がないのが痛いところなのですが、比較対象に揚げるくらいですから、極端に大きいとは考えないことにしました。
ま、後は計算するだけですから、そんなに大変でも何でもないっす。
……とはいいつつも、「州国面積=Z2 +XZ√2」で、二次方程式になってしまった。そりゃ、解けなくはないけれども「解の公式」なんて実生活で使わないから忘れてしまってましたよ。
もっとも、知らなくても関数電卓があれば解けるんですけどね〜。
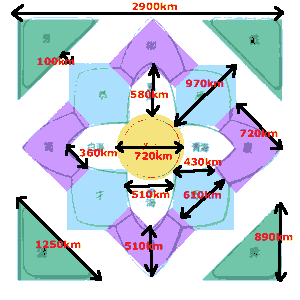
一国面積≒40万km2(候補1)
一国面積≒50万km2(候補2)
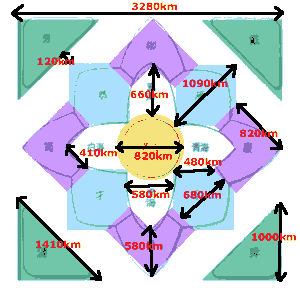
一国面積≒60万km2(候補3)
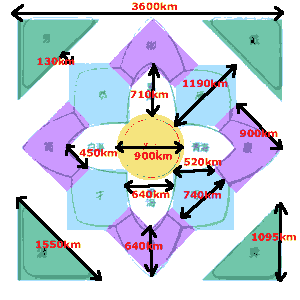
で、意外なことに内海寸法から考えた帆船速度ってのが、平均3-5ノットって計算されました。……なんとも現実的な値にみえます。
ただ、いくら起伏が激しくても740kmに四ヶ月かかるってのは……どんなもんだろう? 東京-京都を往復したって、四ヵ月はかからないと思うのに……。
十二国世界全体の広さって、居住区内虚海を含めても、南極大陸の広さくらいでした。
日本と中国の間にあるらしいので、それでも十分でかいんだろうけれども、確かに「箱庭」(陽子談)っぽい感じがしますね、コレが世界のすべてならね。
おわりに。
よくまぁ、こんなアホなこと真剣に考えたよ。と、自分で突っ込みたくなりました。
誰か考えていてくれれば、こんな計算しないですんだのになぁ……ってなもんですよ。
で、書いたあとにもう一度探してみたら、「十二国記世界の納得のいく理由を考える」
ってのの一部分(№162付近)が、広さや距離について結構言及してました。
それでも陥るのは、「海路と陸路のギャップ」です。で、仮説を立ててみました。
1)十二国記世界の科学力(自然力か?)に期待して、帆船が10ノット以上で走りまくり。
2)十二国記世界全土が、縮小したら屋久島以上の起伏を有していて国境山岳地帯は日本アルプスどころか本家アルプス並み。
……のどちらかってことで。
私は後者を採用したことになるけど、陽子の感想によれば、「土地は起伏が多く、山は概して険しく高い。」(「月の影 影の海」より)とあるし、王宮のあるところなんてアホみたいな山の上だから、こっちが正解臭い雰囲気はムンムン。こうなると、芳の主要産業、牧畜なんて、きっと「アルプスの少女ハイジ」みたいなんだろうな〜。
ま、実際これ考えた感想は、2003/10/26の日記(?)の通りです。
とりあえず、十二国記の二次創作なんてやっている人たちの参考になったらいいかな〜? なんて気軽に考えています。 |