＊ある図形の面積について＊

update:2003/05/12

　[はじめに]
　この問題は，わたしが中学３年（1962年ごろ）のときに，同級生から黒板に書いて出された問題です。当時はまったく解けなくて悔しい思いをしたのを覚えています。以来，時々思い出しては取り掛かっていたような記憶がありますが，納得の行く解答は得られなかったようです。その後，さまざまな数学の本や教科書を見ても，同じ問題を見たことがありません。あの同級生（たぶんＵ君）はどこからこの問題を持ってきたのだろうか（あるいはオリジナルか？）、40年来のナゾです。
　月日が流れて，とうとうこの問題に「ケリをつける」つもりで「最終解答」を仕上げました。以下、その解答です。興味のある方はご覧下さい。

（問）
１辺がの正方形OABCで，Cを中心にCOを半径として正方形の内部に4分円を描く。次にOAの中点をDとし，Dを中心にDOを半径として正方形の内部に半円を描き，二つの弧のO以外の交点をEとする。このとき，弧OEB,OEAにはさまれた部分の面積を求めよ。

（解）　求める面積Sを線分OEによって上下に分け、下をP，上をQとする。
　　　
　　　．

よってPの面積は，
　　　　　　
　また，
　　　　　　
　　　　　　
であるから，Qの面積は，
　　　　　　
　よって求める面積Sは，
　　　　　　

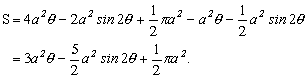
　ここで，　を求めてみよう。△COEで余弦定理より，
　　　　　　

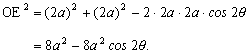
　同じく　△DOEでも，
　　　　　　
　この二つの式から，
　　　　　　
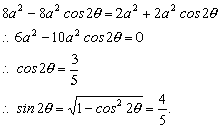
　これを先ほどのSの式に代入すれば，
　　　　　　
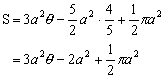
となる。
　さて，次はこの式の中のであるが，半角公式によれば，
　　　　　　
　となるから，は三辺が　　の三角形のつくる角である。上の図でいえば△OEFである。従って解答としては次のように書かなくてはならない。
　　　　　　

　[おわりに]
　これで一応解決なんですが，何となくすっきりしないのは答が美しくないからです。何といってもがあるのが気に入らない。実際に計算しようとすると，三角関数の逆関数が必要になり，などという数を使わなくてはなりません（例：＝10 とすれば，S=24.043...）。まあ，三角関数の逆関数も初等（「超越」だけど）関数だからこの解き方も「初等的」といえばいえるのでしょうが・・・
　これ以上進めようと思えば，このが三角関数の逆関数を用いずには表わせないことを証明しなくてはならない。わたしのすっきりしない気持を納得させるにはそこまで行かなくてはならないのかもしれません。Q.E.D.