����s��ϕ��ɂ���
2002/11/06�@���j�@
�́C�̂��钆����Ƃœ����Ă����킽���́C���̉�Ђ̍H�꒷����Ƃ���u�K��ɔ��N�Ԓʂ��悤�ɖ�����ꂽ�D���̍u�K��́C��Â͖Y�ꂽ�����̒�����Ƃ�ΏۂɁC�����̍Ő�[�̋Z�p�Ɨ��_�������悤�Ƃ������̂ł������D�킽���͂����ōu�t�̂ЂƂ�ł�������w�̕��c���Y�搶�́u�H�Ɛ��w�v�Ƃ����u�`��M�S�ɒ����C�搶����L�O�Ƃ��Ċ�g�S��210�u���ϕ�����v�i�͖�ɎO�Y���E��g���X1962�N�j�Ƃ����{��Ղ����D����͂킽���ɂƂ��č����Ȃ��Ă͂Ȃ�Ȃ����̂ɂȂ��Ă���D���̏��_�́C���̒��̂�����ɂ��ďq�ׂ����̂ŁC���Z�O�N�̐��V�C���Ȃ킿�u���ϕ��C�����ϕ����ł�����x�̃��x���ł���Η������Ă��炦��Ǝv���D
��g�S��210�u���ϕ�����v�i�͖�ɎO�Y���E��g���X1962�N�C�ȉ��e�L�X�g�Ƃ����j��160�y�[�W��9(2)�ɁC
![]() �c�c�c�c�c�c�c�c�i1�j
�c�c�c�c�c�c�c�c�i1�j
��ϕ��i�s��ϕ��j����Ƃ�����肪�������D���̖��̑O�̕����ł������̃e�N�j�b�N����������Ă��āC���̕��@��p���ĉ����Ƃ������K���ł���D�����̉́C
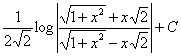 �c�c�c�c�c�c�c�c(�Q)
�c�c�c�c�c�c�c�c(�Q)
�ƂȂ��Ă����D
�@���āC���̊��͖������i�����̒���x������j�Ȃ̂ŁC������������߂ɂ͗^����ꂽ����L�����ɒ����Ȃ��Ă͂Ȃ�Ȃ��D�ȉ��͂��̃e�L�X�g�ɏЉ��Ă�����@�ł���D
�܂��C![]() �Ƃ����ƁC
�Ƃ����ƁC![]() �C
�C ![]() �C�܂��C
�C�܂��C ![]() �C
�C![]() �C����āC
�C����āC
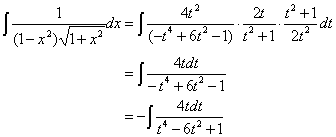
�ƂȂ��ėL�����̐ϕ��ɂȂ�D
�ł���߂ɂ��̖�����������Đϕ����Ă������͂����Ȃ��D���������e�L�X�g�̂P��P��ɂ͏��w�҂���J���Ȃ��悤�i����ł���J���邪�j�אS�̍H�v������Ă���D�����鉤��������킯�ł���B�����ɂ������Ă킽���͐��X�̊ԈႢ��Ƃ����̂����C����͂��܂�ɒp���������̂ŗ����C���ʂ����������Ă���D���݂ł��킽���̎��͂͂��̒��x�̐ϕ���S�͂ł���Ɖ����Ƃ������x�ŁC40�N���O�̓��发�ɏ������Â��������Ȃ��D�ނ���C�����������ɒx��Ă��邩���v���m�炳������ł���D
�@���̕���́C![]() �ƕό`�ł���̂ŁA�����ł����
�ƕό`�ł���̂ŁA�����ł����![]() �ƒu��������ƁA
�ƒu��������ƁA![]() ������C
������C
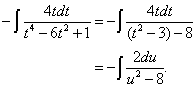
�@���͂��̕���������ɒ����悢�̂ł��邪�C�����͌����ł��܂���B�����
![]()
�ł���D����ɂ���āC
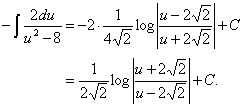 �c�c�c�c�c�c�c�c�i�R�j
�c�c�c�c�c�c�c�c�i�R�j
�@���Ƃ͂������ɖ߂��A��������ɂ��ǂ������̂����A����Ă݂�ƁA
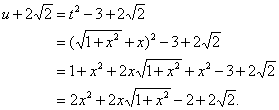 �c�c�c�c�c�c�c�c(�S)
�c�c�c�c�c�c�c�c(�S)
���l�ɁA![]() �ł��邩��C(3)��
�ł��邩��C(3)��
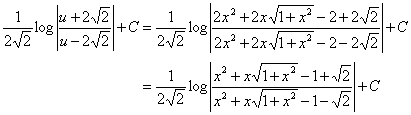 �c�c�c�c�c�c�c�c�i�T�j
�c�c�c�c�c�c�c�c�i�T�j
�ƂȂ��āA��q���������̉�(2)�ƈႤ���A����͂���ō����Ă͂���̂ł���i�ǂ�������������(1)�ɂȂ�j�D�m���ɉ̕������̎������Ⴂ�̂ŁA(5)�͂܂����S�Ƃ͂����Ȃ����ƂɂȂ�D
�@�ł́C�ǂ�����悢���D�܂��C�قȂ�����������ē������͐ϕ��萔�����̈Ⴂ�ł��邩��C(2)����(5)�������Ă݂�B
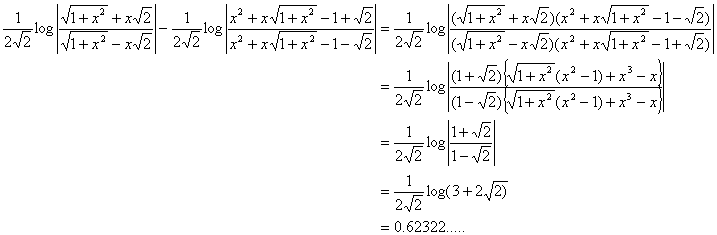
�ƂȂ��Ċm���ɒ萔�ł���D�܂�C(2)��(5)�̊W�́C![]() �ƂȂ�D�䂦�ɗ��ӂ��������Γ������̂ɂȂ��āC(1)�̕s��ϕ��̓����Ƃ��Ă͂ǂ�����������D���̒萔���݂�ƁC�^����
�ƂȂ�D�䂦�ɗ��ӂ��������Γ������̂ɂȂ��āC(1)�̕s��ϕ��̓����Ƃ��Ă͂ǂ�����������D���̒萔���݂�ƁC�^����![]() �ƂȂ��Ă��āC��̌v�Z��(4)�̂Ƃ���Ɏ��������o�Ă���D�����ɍH�v�̎d��������悤�Ɍ�����D������(3)�����蒼���Ă݂悤�D
�ƂȂ��Ă��āC��̌v�Z��(4)�̂Ƃ���Ɏ��������o�Ă���D�����ɍH�v�̎d��������悤�Ɍ�����D������(3)�����蒼���Ă݂悤�D
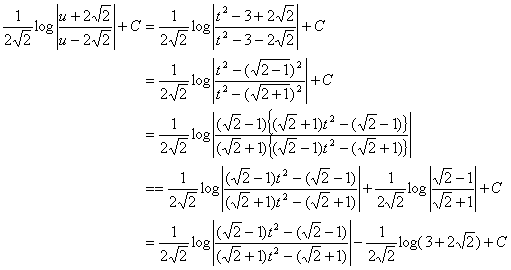
�ƂȂ���![]() ���O�ɏo�����Ƃ��ł����D���Ƃ�
���O�ɏo�����Ƃ��ł����D���Ƃ�![]() �������Đ��������(2)�̉Ɠ����ɂȂ�̂ł���D
�������Đ��������(2)�̉Ɠ����ɂȂ�̂ł���D
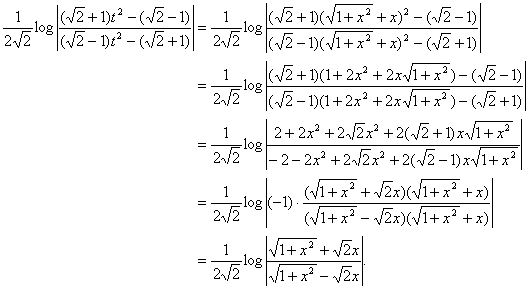
�@�ȏ�ł߂ł����ł��邪�C����͐������邩��ł����̂ł����āC���ꂪ�Ȃ���킽���͂��Ԃ�(5)�̂܂܂ł��̖����I���Ă���Ǝv���D�i�T�j�ŏI��邩(2)�ɂ܂Ŏ��邩�̈Ⴂ�́C���w�̌����ł͖{���I�Ȏ����ł���Ǝv���D���̖��Ɋւ��Ă͎��͉�������������C�������������̉�����������d�������������̂ł���D
�i2002/11/09�@11�F25A.M.�j