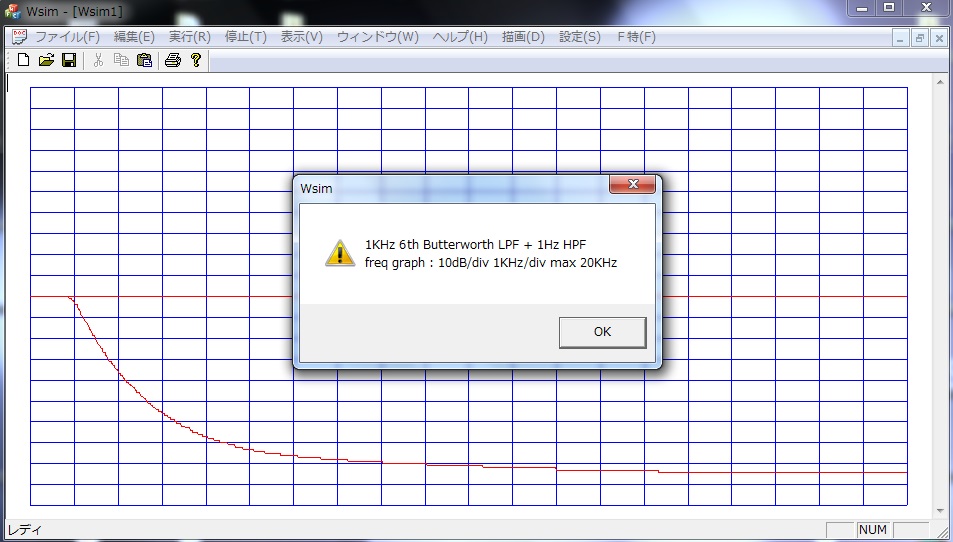
アナログ回路の特性をソフトウェアによりシミュレーションする方法として、離散時間差分方程式による数値計算法を紹介します。
アナログ回路のシミュレーションは回路データを入力して計算する方法が一般的ですが、LPF のような多項式で表記できる場合は、離散時間系の差分方程式を使用して高速な計算ができます。また、ディジタルフィルタのような計算遅延のない出力が得られます。添付のソースコードの特性多項式の定数を変更すれば、容易に他の特性をシミュレーションできます。(バターワースと0.1dB/0.5dB/1.0dB チェビシェフ)
6次バタワースLPF の伝達関数 $G(s)$
\[ G(s) = \frac{1}{s^2+0.51764s^2+1}\cdot\frac{1}{s^2+1.41421s^2+1}\cdot\frac{1}{s^2+1.93185s^2+1} \]
下記に離散時間差分方程式による数値計算式の導出方法を示します。
2次のLPF 伝達関数 $G(s)$
\[ G(s) = \frac{a_2}{s^2+a_1s^2+a_2} \]
1入力1出力系の連続時間系の状態方程式、$t\geq0$
\[ \dot{x}(t) = Ax(t) + bu(t) \\ y(t) = c^Tx(t) \]
可制御標準形で構成した時の係数行列 $A$、駆動行列 $b$、出力行列 $c$
\[ A = \left( \begin{array}{ccc} 0 & -a_2 \\ 1 & -a_1 \end{array} \right), b = \left( \begin{array}{ccc} a_2 \\ 0 \end{array} \right), c = \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right) \]
離散時間系の状態方程式, $k=0,1,\cdot\cdot\cdot$
\[ x((k+1)T) = \Phi(T)x(kT) + \Psi(T)u(kT) \\ y((k+1)T) = c^Tx(kT) \]
但し、$ \Phi(T) = \mathcal{L}^{-1}[(sI-A)^{-1}] $、$ \Psi(T) = A^{-1}( \Phi(T)-I )b $、$ I = \left(\begin{array}{ccc} 1 & 0 \\ 0 & 1 \end{array}\right) $
上記の行列係数を計算することにより、サンプリング時間 $T$ の離散時間系の差分方程式が得られます。
\[ x_1((k+1)T) = e^{-\frac{a_1}{2}T}(cos(\omega T)+\frac{a_1}{2\omega}sin(\omega T))\cdot x_1(kT)-\frac{a_2}{\omega}e^{-\frac{a_1}{2}T}sin(\omega T)\cdot x_2(kT)+( (a_1(1-e^{-\frac{a_1}{2}T}cos(\omega T))+\frac{a_2-\frac{a_1^2}{2}}{\omega}e^{-\frac{a_1}{2}T}sin(\omega T) )\cdot u(kT) \]
\[ x_2((k+1)T) = \frac{1}{\omega}e^{-\frac{a_1}{2}T}sin(\omega T)\cdot x_1(kT)+e^{-\frac{a_1}{2}T}(cos(\omega T)-\frac{a_1}{2\omega}sin(\omega T))\cdot x_2(kT)+( 1-e^{-\frac{a_1}{2}T}(cos(\omega T)+\frac{a_1}{2\omega}sin(\omega T)) )\cdot u(kT) \]
\[ y(kT) = x_2(kT) \]
但し、$ \omega = \sqrt{a_2-\frac{a_1^2}{4}} $

