Polar 符号の対数尤度比(log-likehood ratio: LLR)を使用する復号法
Polar 符号について、下記の GitHub にある PolarC (C++ surce code)を分析することにより、符号化と復号方法を詳解します。
PolarC は、PolarCode.cpp、PolarCode.h、main.cpp の 3 つの source code で記述されています。コンパイルは Visual Studio Code + MinGW の環境で、下記のように g++ を呼び出して行えます。
- g++ -o PolarC.exe main.cpp PolarCode.cpp
PolarC の Polar 符号は、情報 bit = 1024 = 2^10、符号化 bit = 2048 = 2^11、符号化率 = 1/2 です。
復号は Eb/N0 をパラメータとして、Block Error Rate を出力します。(真値表示、% 表示は 100 倍)
Block Error Rate は、1 つの符号に対して 100回行い、total 10個の符号に対して繰り返し、total 1000回の復号結果から計算しています。
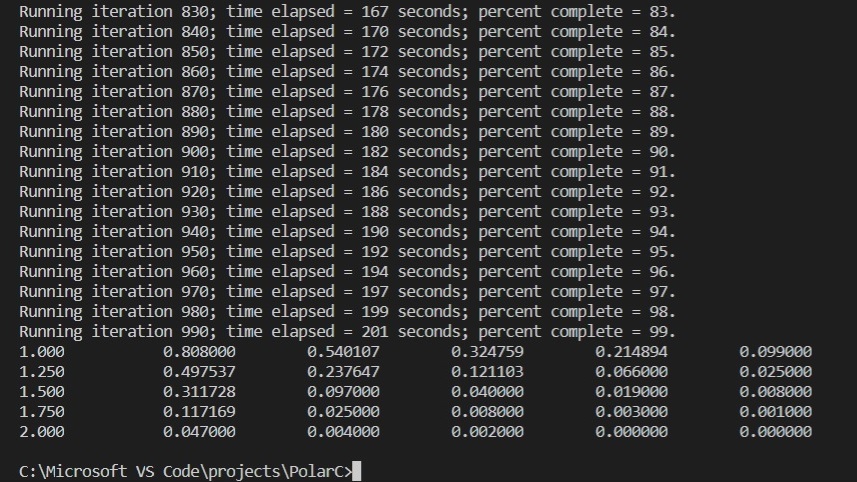
Eb/No は、1.00 から 2.50 まで、0.25 step (unit:dB)
Block Error Rate は、LLR list size = 1、2、4、8、32 に対して各々計算されています。
list は、推定した符号化 bit の候補 list です。この中から LLR が最も小さい list が復号 bit として選択されます。
符号化
符号化は、最初に 凍結 bit (frozen bit) と呼ばれる bit を付加した後、XOR (排他的論理和)による符号化を n 回繰り返します。
次に、bit の並びをある規則に従って入れ替えを行い、符号化 bit を得ます。
PolarC.cpp の中では、encode() で符号化を行っています。
凍結 bit (frozen bit) の付加
符号化率 1/2 より、情報 bit と同じ数の凍結 bit を追加します。
PolarC.cpp の中では、initialize_frozen_bits() で 配列 (vector) _frozen_bits に、情報 bit は "0"、凍結 bit は "1" を設定します。
符号化 bit = 16 (n = 4) の設定 : _frozen_bits[0:15] = 1 1 1 1 1 1 1 0 1 0 0 0 0 0 0 0
符号化 bit = 32 (n = 5) の設定 : _frozen_bits[0:31] = 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 0 1 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0
情報 bit (info bit) の並び
復号処理は 符号化 bit を復号する為、情報 bit の並び替えは必要ないと思いますが、PolarC.cpp の中では、
initialize_frozen_bits() で 配列 (vector) _channel_order_descending に info bit の番号を設定します。
符号化 bit = 16 (n = 4) の設定 : _channel_order_descending[0:15] = - - - - - - - 4 - 7 6 3 5 2 1 0
符号化 bit = 32 (n = 5) の設定 : _channel_order_descending[0:31] = - - - - - - - - - - - 14 - 13 11 5 - - - 12 - 10 9 4 15 8 7 3 6 2 1 0
XOR (排他的論理和)による符号化 (n 回繰り返し)
2 bit (bit0 : 偶数 bit、bit1 : 奇数 bit) 毎に XOR (排他的論理和) 演算を行い、演算結果を出力 bit0、入力の奇数 bit を出力 bit1 とする。
同様の演算を 偶数 bit、奇数 bit の 2 bit 毎に n 回繰り返します。
PolarC.cpp の中では、encode() で 配列 info_bits_padded に符号化を行っています。
bit の並びの入れ替え
Polar 符号化の規則に従って、bit の入れ替えを行います。
create_bit_rev_order() で 配列 (vector) _bit_rev_order に 配列 info_bits_padded bit の番号を設定します。
符号化 bit = 16 (n = 4) の設定 : _bit_rev_order[0:15] = 0 8 4 12 2 10 6 14 1 9 5 13 3 11 7 15
符号化 bit = 32 (n = 5) の設定 : _bit_rev_order[0:31] = 0 16 8 24 4 20 12 28 2 18 10 26 6 22 14 30 1 17 9 25 5 21 13 29 3 19 11 27 7 23 15 31
ここまでが、符号化の処理です。
符号化の処理は、汎用化されており、n を変更して実行することができます。
復号
復号は、偶数 bit と奇数 bit に対して下記の対数尤度比(log-likehood ratio: LLR)を計算する。
偶数 bit の $LLR_e(k)、k = 1 ... n$
\[
LLR_e(k) = log_{2}{\frac{exp(LLR_e(k-1) + LLR_o(k-1)) + 1}{exp(LLR_e(k-1)) + exp(LLR_o(k-1))}}
\]
奇数 bit の $LLR_o(k)、k = 1 ... n$
\[
LLR_o(k) = (1 - 2 * C) * LLR_e(k-1) + LLR_o(k-1)
\]
ここで、$C$ は 1つ前に推定された 符号化 bit。"0" の時は加算、"1" の時は減算が実行される。
符号化の時と同様に、偶数 bit は XOR 入力 bit0、奇数 bit は XOR 入力 bit1 に対応する。
LLR は、符号化の XOR (排他的論理和) 演算を出力から入力へ向けて計算される。この様子は、XOR (排他的論理和) 演算を図示すると分かり易い。
奇数 bit の LLR を計算する時に必要な $C$ も、LLR と同様に出力から入力へ向けて計算される。
復号 bit の推定は、LLR から計算された threshold との比較結果から確からしさを示す 2 bit から求める。
この演算は、continuePaths_UnfrozenBit() の中で行われる。
この処理は、複雑なので 候補 list = 1 の時の動作を理解することから始める。
ここまでが、復号の処理です。
復号の処理も、符号化と同様に汎用化されています。
復号の処理は、source code を見ても理解することは難しいので、実行中の配列と変数をモニタすると理解しやすいです。
C++ のコンソールへの出力は、std::cout ... std::endl;
PolarCode.cpp にコンソール出力を追加した修正 version と出力結果、動作確認用の Excel file
2019-11-04
ホーム



